Chapter 1: Introduction to the Puzzle

Presh Talwalkar from MindYourDecisions presents an engaging puzzle about birth years:

This puzzle encourages us to think critically rather than simply guessing. For instance, through some trial and error, we can identify that 2014 works, as the sum of its digits (2 + 0 + 1 + 4) equals 7, and the difference between 2021 and 2014 is also 7. However, let's delve into a more systematic approach!

First, let's clarify the variables. We will designate your birth year as y. Consequently, your age on your birthday in 2021 is given by the equation 2021 - y. Since y is a four-digit number, we can express it as:

y = 1000a + 100b + 10c + d

Where a, b, c, and d represent the digits of y. Additionally, the following holds true:

a + b + c + d = 2021 - y

Given that you are under 100 years old, we conclude that y must be greater than 1921 and less than 2021. Therefore:

• y is an integer
• 1921 < y < 2021

This leads to the initial equations we will work with:

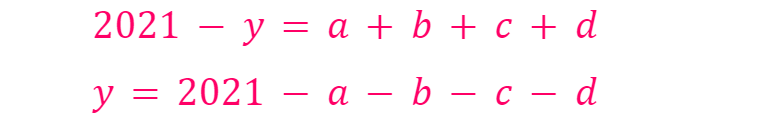
Equation 1

Moreover, we can derive another equation:

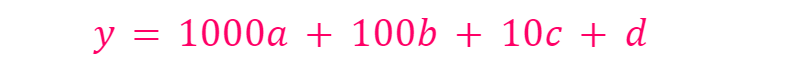
Equation 2

By combining Equations 1 and 2, we arrive at:

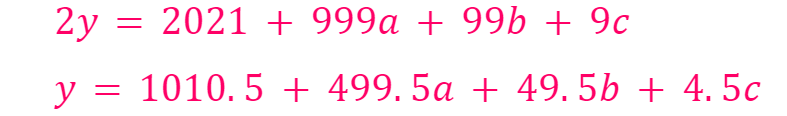
Equation 3

Although this appears challenging with one equation and three unknowns, we can effectively find the solution! Remember that a, b, c, and d can only take values between 0 and 9. Given our constraints, we also know that y is greater than 1921. This means b and c cannot be 9. Therefore, a can only be 1 or 2.

Why do we limit a this way? If a were 0, we would not reach a value of y above 1921, regardless of the values of b and c. Conversely, if a exceeded 2, y would exceed 2021.

Let’s explore both scenarios: