Chapter 1: The Problem Statement

Have you ever wondered if it’s possible to connect two points with just two lines that do not intersect, all while keeping these lines confined within a square?

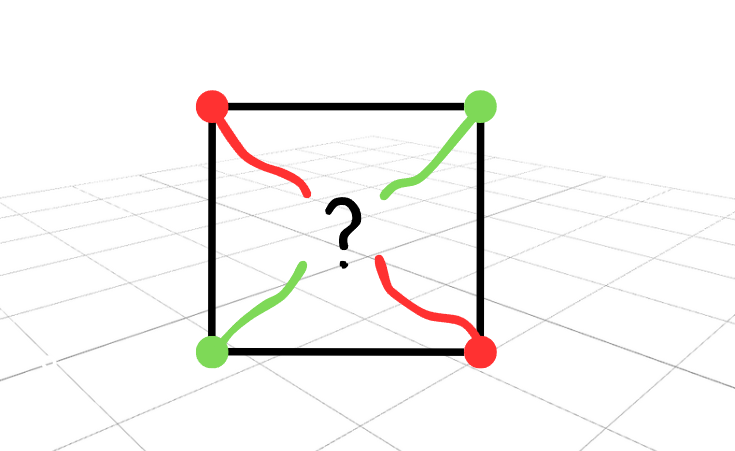
If we weren’t limited to drawing lines inside the square, the task would be simple. However, since we are bound by this constraint, we need to think creatively to arrive at a solution. This challenge appeared on my topology exam, and I initially dismissed it as unfeasible. To my surprise, there was a clever solution!

You might have an inkling of the answer by now, but it’s quite amusing. Take a moment to ponder it, but don’t overanalyze!

Yes, it turns out we can link the two pairs of points with non-intersecting lines. This involves a fascinating mathematical concept known as the topologist’s sine curve. Here’s how it appears:

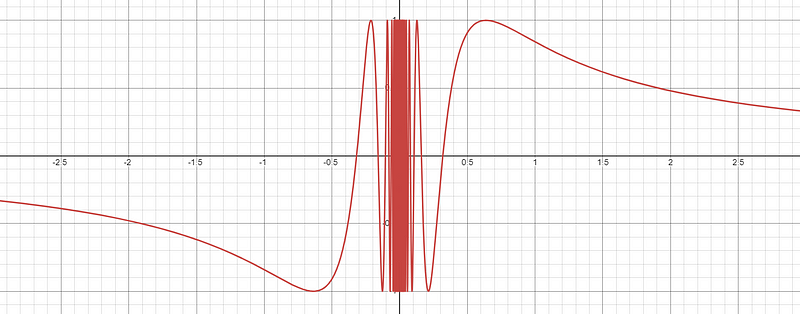
This graph represents the equation ( y = sin(1/x) ). As ( 1/x ) approaches infinity near ( x = 0 ), the curve oscillates infinitely as it nears the y-axis.

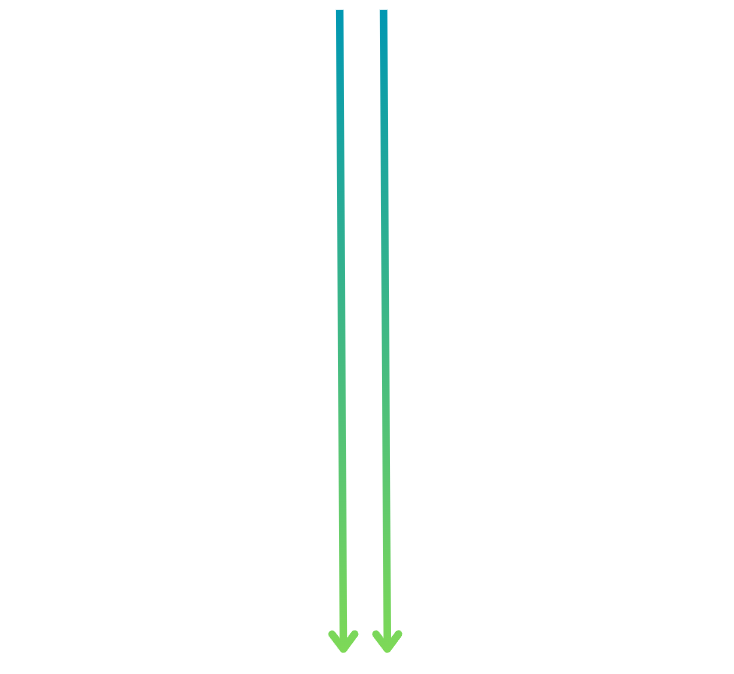
Next, we can truncate the left half of this curve and fit it neatly into our square:

Now, we can manipulate the curve to ensure it fits comfortably within the boundaries of our square. By creating a duplicate of the curve and shifting it slightly downward, we can ensure that the two curves remain non-intersecting. Finally, we connect the endpoints of the curves to the designated points.

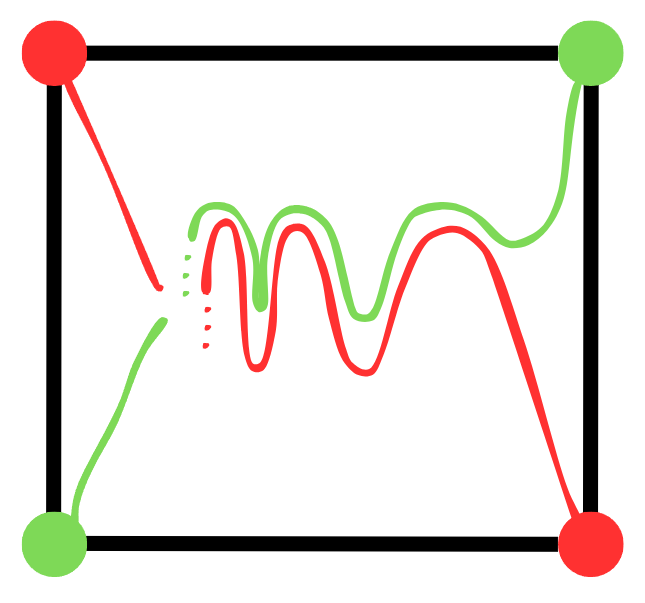
And there we have it! The two pairs of points are successfully connected by two lines that do not intersect. But what’s the reasoning behind this solution? Everything seems logical until we reach the ambiguous point in the image.

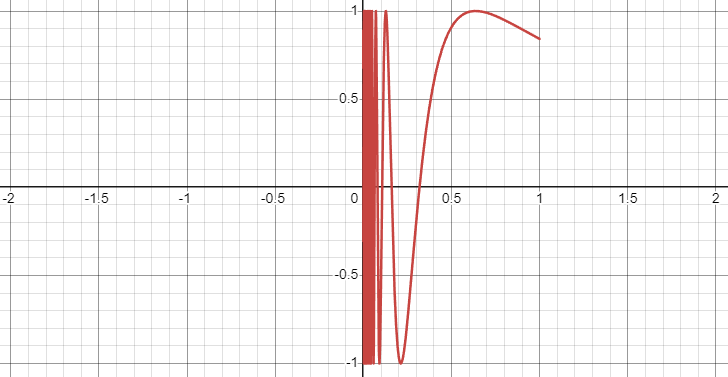
To grasp the underlying concept, let’s take a closer look at the topologist's sine curve with its left half removed:

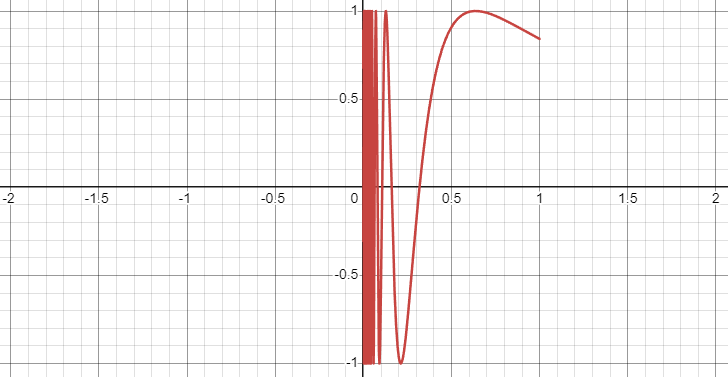
As we approach ( x = 0 ), the curve fluctuates between -1 and 1. If we select any point ( z ) on the y-axis between these two values and choose a small distance ( epsilon ) to the right, we can observe the following:

We’ve identified point ( z ) and a distance ( epsilon ) to the right. The blue line represents the y-axis. It’s important to note that portions of the topologist's sine curve consistently lie within ( epsilon ) of ( z ). Since ( epsilon ) can be made arbitrarily small, we can conclude that there are points on the sine curve that get infinitely close to ( z ). This establishes that ( z ) is connected to the curve.

Hence, any line drawn from ( z ) will remain connected to the topologist's sine curve, allowing us to meet the requirement of connecting the two points as originally intended.

Challenge for the Curious: For those familiar with topology, would it still be feasible to connect the points with disjoint lines if the lines had to be path-connected?

Chapter 2: Visual Explanations

This video titled "How to find the intersection point of two linear equations" provides a visual guide to understanding the concepts of intersections in linear equations.

In this video, "Finding the intersection of two lines without graphing," viewers can learn techniques for determining intersections without the need for graphical representation.