Chapter 1: Understanding Trigonometric Equations

When tackling trigonometric equations, it’s crucial to remember that functions like sin(x) and cos(x) exhibit periodic behavior. This characteristic means there are countless values of x that can satisfy any given equation, leading to an infinite number of solutions. For example, the equation sin(x) = 0 does not solely yield x = 0; it also includes solutions like x = π, x = 2π, x = 3π, x = -π, x = -2π, and so forth, since sin(x) equals zero at all these points. Therefore, we express this as sin(x) = 0 yielding solutions of the form x = nπ, where n can be any integer, positive or negative.

However, when we consider the equation sin(x) = 2, it appears that it should have a solution in a similar manner. The challenge arises from the fact that the sine function is constrained between -1 and 1. This means that no real value of x will satisfy sin(x) = 2. Yet, if we expand our view to include complex numbers, we discover new possibilities. To delve deeper into this, we can express sin(x) using Euler's formula, which I elaborated on in my previous article.

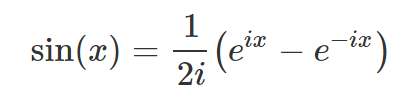
From this expression, we derive the following:

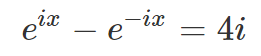
Next, by multiplying both sides by exp(ix), we obtain:

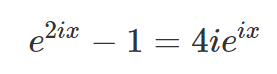
This simplifies to:

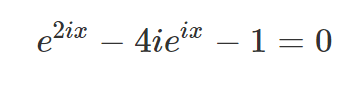
Examining this equation closely, we can substitute:

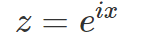
Thus, we arrive at:

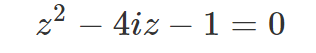
This expression is a straightforward quadratic equation. By applying the quadratic formula, we can find:

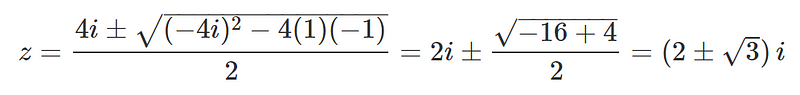
We then proceed to solve for x:

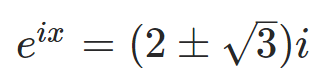
This can be rephrased as:

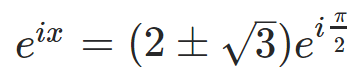
Here, we express the imaginary unit i in polar coordinates, where its angle is π/2. This can be resolved using logarithmic functions:

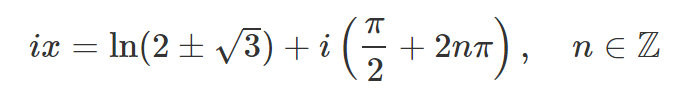
In this expression, n denotes an integer, and the term 2nπ arises because exp(iπ/2) is equivalent to exp(i(π/2 + 2nπ)) for any integer n, owing to the rotational nature on the complex plane, which I discussed in my earlier article. Consequently, we find that:

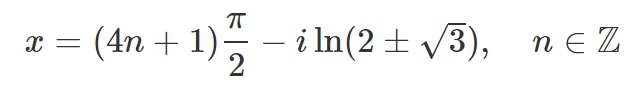
represents the complete set of solutions to the equation sin(x) = 2. Although it may seem surprising that such an equation has solutions, it’s vital to keep in mind that the realm of complex numbers reveals many unexpected possibilities.

Chapter 2: Video Explanations

The first video, A Non-Standard Trig Equation | sin(x)=2, provides a detailed look at the implications of this equation within trigonometry.

The second video, Solving a trig equation involving sin(x/2), explores further techniques for resolving similar trigonometric equations.