Chapter 1: Introduction to Differential Equations

When I began my journey into differential equations, it felt surprisingly easy as it builds upon my foundational understanding of integration from calculus. Let's examine and tackle a specific problem. This differential equation challenges our grasp of separation of variables, a fundamental method in ordinary differential equations.

One handy tip is to combine related terms into a single entity.

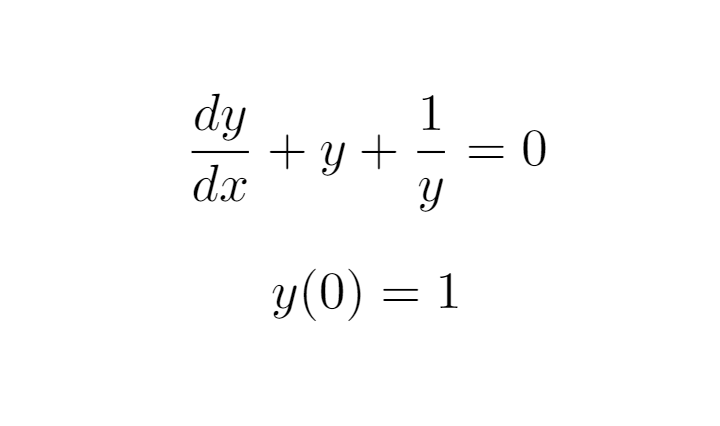
Next, we’ll move the fraction to the right-hand side.

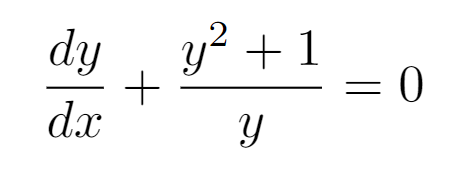
At this stage, you should have a clear idea of how to continue. By arranging all the y's and x's on their respective sides, we arrive at this formulation.

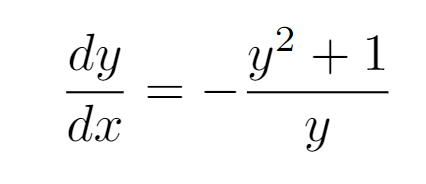
Now here’s a challenge: can you figure out the integral on the left side? (Hint: the numerator might be expressible as a derivative of the denominator!) After integrating both sides, we will find the following result.

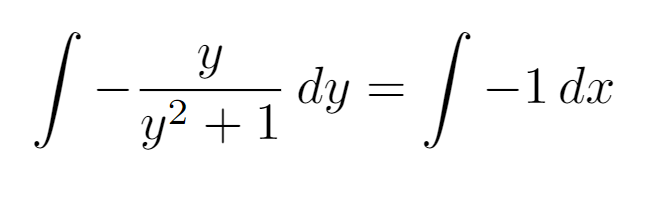
And remember to include the constant of integration, c! With our initial condition y(0) = 1, we can derive the subsequent expression.

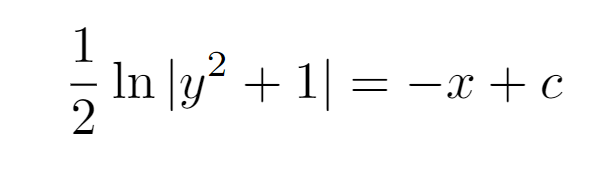
Ultimately, we want to rearrange the equation to isolate x.

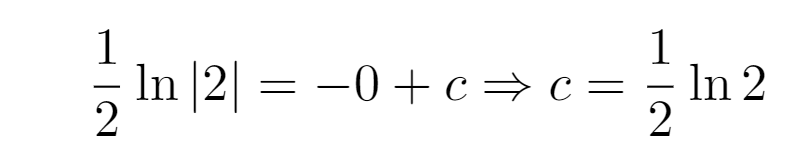
And that’s a fitting stopping point for our exploration. There lies our solution. Isn’t it fascinating? I’d love to hear your thoughts—feel free to comment below!

This first video, titled "Differential Equations 1: Oxford Mathematics 2nd Year Student Lecture," provides a detailed introduction to the subject matter.

The second video, "What is a DIFFERENTIAL EQUATION?? Intro to my full ODE course," offers a thorough introduction to differential equations, setting the stage for more advanced concepts.

Chapter 2: Engaging with Math Puzzles

As we conclude this segment, don't forget to explore the intriguing world of math puzzles.

Math Puzzles

The best math puzzles on Medium

Algebra, Geometry, Calculus, Number Theory, and more

Share this with your friends and...

Thank you for your time! If you found this article helpful, please show your support by giving it a clap.

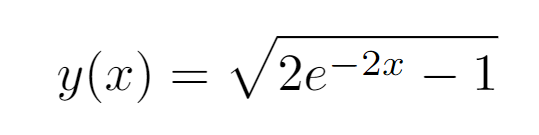
If you’re feeling generous, consider buying me a coffee as a token of appreciation. Your support means the world to me!

Love, Bella