Chapter 1: Introduction to the Puzzle

This engaging geometry puzzle was shared by Catriona on Twitter, who is known for her delightful and visually appealing geometry challenges. It’s one of those straightforward yet gratifying puzzles that can captivate your mind.

To get started, here's a tip: try sketching some lines. I encourage you to take a moment, grab a pen and paper, and attempt to solve it before moving on to the solution!

Section 1.1: Understanding the Basics

To solve this puzzle, we begin with the knowledge that the area of each small circle is 1. We can determine its radius using the formula ( A = pi r^2 ).

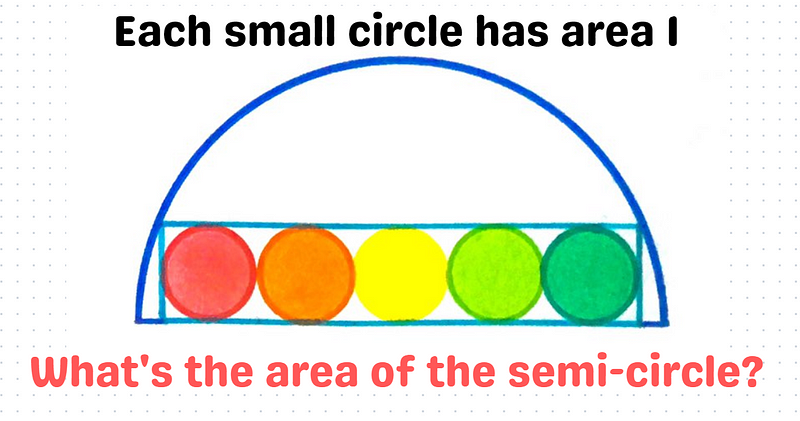
With this information, we can construct a rectangle and form a right-angled triangle as illustrated below.

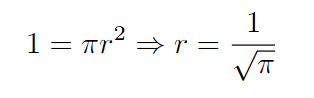
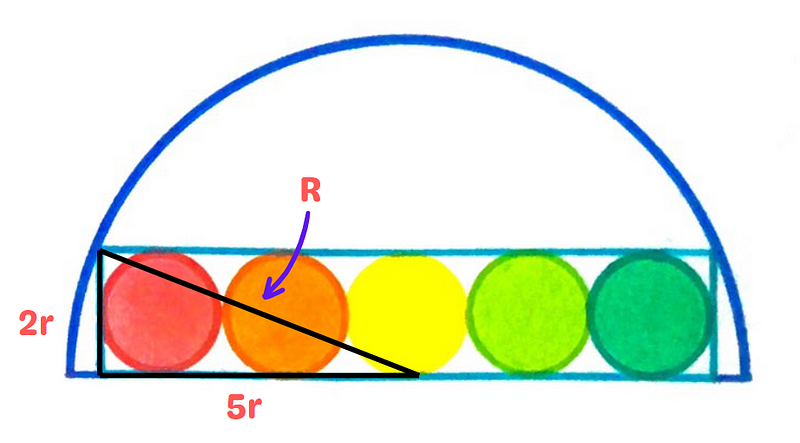
Section 1.2: Establishing Relationships

Let’s denote ( R ) as the radius of the semi-circle. Our objective is to express ( R ) in terms of ( r ). By applying the Pythagorean theorem, we arrive at a crucial relationship.

Now that we have both ( r ) and ( R ) defined in terms of ( r ), we can utilize the semi-circle area formula ( A = frac{1}{2} pi r^2 ) to reach our conclusion.

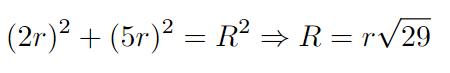
And there’s our final answer! Isn’t it fascinating?

What was your thought process while solving this? I’d love to hear your insights in the comments below!

Chapter 2: Exploring More Puzzles

If you enjoyed this puzzle, don't forget to check out some of the best math puzzles available on Medium. They cover various topics, including Algebra, Geometry, Calculus, and Number Theory.

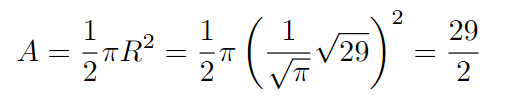
Thank you for taking the time to read this article. If you found it informative, please consider giving it a clap!

If you appreciate my work and would like to support my writing, feel free to buy me a coffee. Your generosity means a lot and helps me continue creating content for you.

Thank you!