The Number Line

Traditionally, we visualize numbers on a number line that extends from negative infinity to positive infinity, with zero positioned at the center. Notable numbers like e and π are found along this continuum, which we refer to as the set of real numbers, denoted by ℝ.

This set comprises various well-explored subsets, including the natural numbers ℕ = {1, 2, 3, …}, whole numbers ℤ = {… -2, -1, 0, 1, 2, …}, and rational numbers, which can all be expressed as fractions of two integers, represented by ℚ.

Before delving deeper, it's essential to clarify some notation. If we say that a set of numbers A is included in another set B, we write A ⊆ B. Within this framework, we can illustrate:

ℕ ⊆ ℤ ⊆ ℚ ⊆ ℝ ⊆ ℂ

Here, natural, whole, rational, real, and complex numbers are represented in sequence. Importantly, every whole number can be expressed as a fraction, meaning all whole numbers qualify as rational.

Around 500 B.C., there existed a group known as the Pythagoreans, who held the belief that all numbers were rational. However, one of their own philosophers, Hippasus, demonstrated that the square root of 2 is not a rational number.

This proof is not only elegant but also a landmark moment in the history of mathematics. The Pythagoreans were so incensed by Hippasus's revelation that they allegedly drowned him.

To clarify, Hippasus established that:

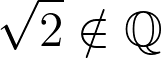
This proof indicates the existence of numbers that cannot be represented as fractions of whole numbers, which we refer to as irrational numbers.

The set of irrational numbers is a subset of the real numbers, containing many celebrated mathematical constants such as the square roots of natural numbers, e, π, and the golden ratio φ. This distinction creates two separate, non-overlapping categories within the real numbers: rational and irrational.

While both rational and irrational numbers are infinite sets, mathematicians emphasize that this concept of infinity is not uniform. Thanks to Georg Cantor’s work on cardinality, we understand that different infinities exist, and notably, the set of irrational numbers is a larger and distinct type of infinity compared to the set of rational numbers.

Transcendental Numbers

Interestingly, some irrational numbers emerge as roots of polynomials with integer coefficients. For instance, the square root of 2 serves as a root of the polynomial f(x) = x² - 2. These numbers are classified as algebraic, which also includes all rational numbers, as every fraction is a root of a linear polynomial in the form ax + b. Even complex numbers can be algebraic; for example, the imaginary unit i is a root of the polynomial x² + 1.

Many famous irrational numbers are algebraic, such as the golden ratio φ, which is a root of the polynomial x² - x - 1.

Conversely, a real number that is not algebraic is termed transcendental. Since these two categories do not overlap, the real line can be divided into two distinct subsets: algebraic numbers and transcendental numbers.

For a long time, transcendental numbers were only hypothesized until Joseph Liouville proved their existence in 1844 and even constructed an example of such a number.

Georg Cantor demonstrated through straightforward reasoning that there are countably many algebraic numbers (indicating that their cardinality matches that of the natural numbers). Given that there are uncountably many real numbers—also shown by Cantor using his famous diagonal argument—it follows that the vast majority of real numbers are transcendental.

Until the late 19th century, transcendental numbers had primarily been discovered through construction rather than proof. However, this changed dramatically when Ferdinand von Lindemann made a groundbreaking contribution.

He established the following:

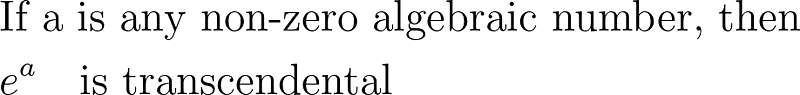
Understanding the implications and elegance of this theorem is crucial. It allowed for the identification of infinitely many transcendental numbers, many of which were previously known yet had not been recognized as such.

The contrapositive form of this theorem is also insightful, stating:

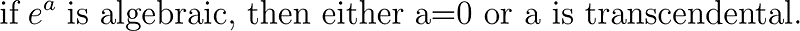
The Most Famous Equation in Mathematics

Lindemann was certainly aware of Euler’s Identity, which many consider the most beautiful equation in mathematics. It is expressed as follows:

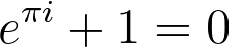
By applying the contrapositive version of Lindemann’s theorem, we conclude that e^i is transcendental. Since i is algebraic, it follows that e must also be transcendental. This conclusion arises from the fact that algebraic numbers are closed under multiplication, meaning if a and b are algebraic, then ab is also algebraic. While this may not be immediately evident, it can be demonstrated using symmetric polynomials and some ingenuity.

Subsequently, e has been proven to be transcendental through various methods.

Future Challenges

Despite our understanding, the realm of transcendental numbers remains largely enigmatic. We lack effective techniques for demonstrating the transcendence of many candidates. Notably, we still do not know whether eπ or e + π is transcendental. Additionally, the status of the Euler-Mascheroni constant γ remains unclear; we have not even established whether it is irrational.

This ignorance is quite troubling, especially considering the significance of these numbers. Overall, our knowledge of transcendental numbers is scant, particularly when weighed against their abundance. Even identifying a number as irrational does not significantly aid in proving its transcendence.

If a mathematician successfully proves a previously unknown transcendental number, they will undoubtedly achieve fame.

As Georg Cantor wisely remarked, "In mathematics, the art of asking questions is more valuable than solving problems."