Chapter 1: Understanding Delivery Challenges

In this section, we will delve into the intricacies of resolving complex mathematical issues within the transportation sector.

The challenges of last-mile delivery are critical for minimizing overall supply chain expenses. With nearly 30% of total supply chain costs arising from this segment, meticulous delivery planning can significantly reduce transportation expenses and enhance competitive positioning.

Navigating real-world delivery logistics can be exceedingly difficult. For instance, a straightforward route optimization scenario involving a single vehicle with 50 stops presents 30 million times more combinations than there are hydrogen atoms in the sun! Moreover, various vehicles come with distinct operational costs, load capacities, and driver skill levels, necessitating timely deliveries while minimizing costs.

As competition intensifies, large corporations like Amazon continually redefine customer expectations for delivery services. To achieve meaningful cost reductions, businesses must factor in vehicle capacities and types (such as cold-chain capabilities), distance (cost per mile), time-related expenses (driver wages), and specific vehicle features (like dock lifts).

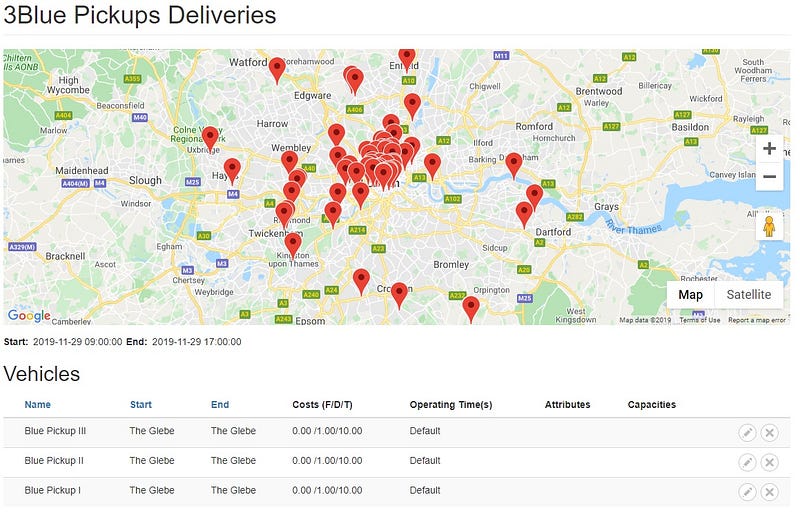
Consider a fictional delivery service called 3Blue Pickups, which comprises three blue pickup trucks tasked with visiting 60 locations for a mix of deliveries and returns.

Here’s a preliminary overview of the delivery map:

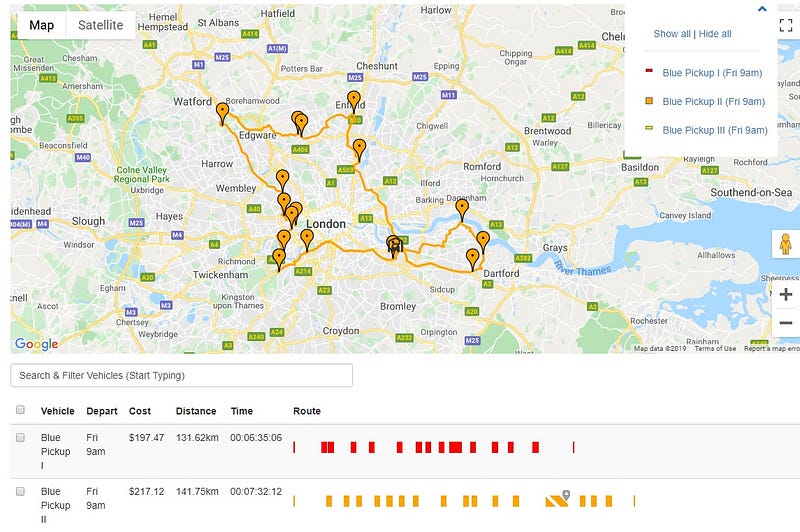
Without any strategic delivery planning, the ideal route for these three vehicles, given the constraints from 9 AM to 5 PM, appears as follows:

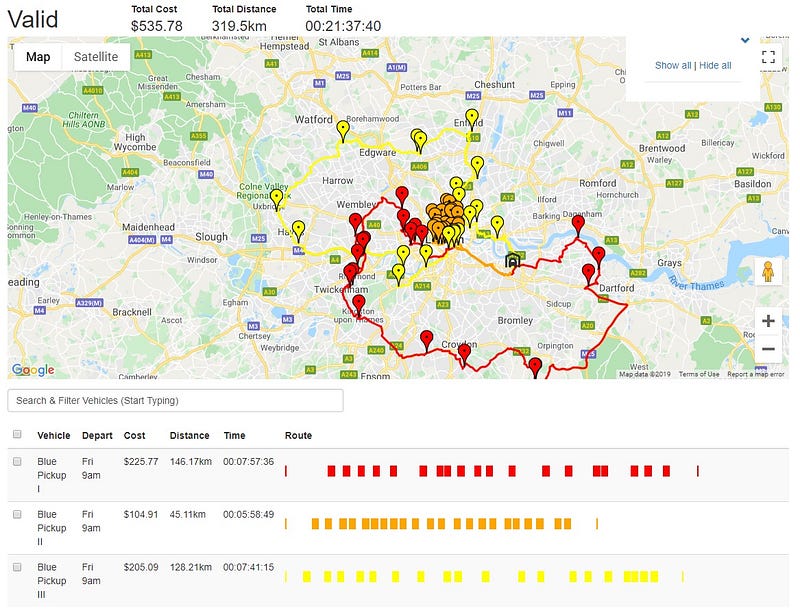
This plan shows that the three vehicles can feasibly cover all locations within the allotted time frame. However, two of the vehicles are close to exhausting their eight-hour limit, indicating that while it is technically possible to visit every stop, the route plan is on the edge of impracticality. Without this analysis, our hypothetical company could find itself needing to rent an additional vehicle, incurring significant costs.

Nevertheless, this theoretical optimal route lacks utility in a real-world scenario since it doesn't account for the necessary deliveries and pickups. For example, if Blue Pickup II were to make too many stops and exceed its capacity, it would need to return to the depot mid-route, resulting in extended travel time and increased costs due to driver overtime.

To make route planning more applicable to real-world conditions, it is crucial to consider carrying capacities.

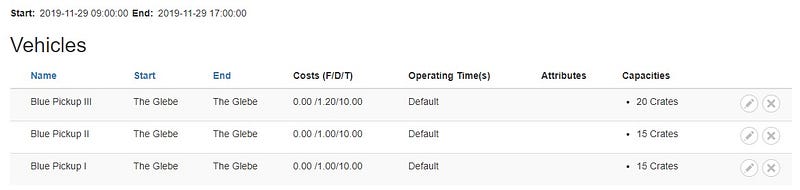
In this scenario, our blue pickups are now assigned specific carrying capacities measured in crates. For example, Blue Pickup III can hold 20 crates due to its larger size, while the other two smaller vehicles can each carry 15 crates. The cost per mile for Blue Pickup III stands at $1.20, whereas the smaller pickups are billed at $1.00 per mile. This gives our fleet a total capacity of 50 crates.

Next, we can introduce a delivery manifest outlining the required deliveries and pickups at each location. For simplicity, we will start with delivering one crate to each location, totaling 60 crates, which exceeds our fleet's carrying capacity.

Here’s the updated result:

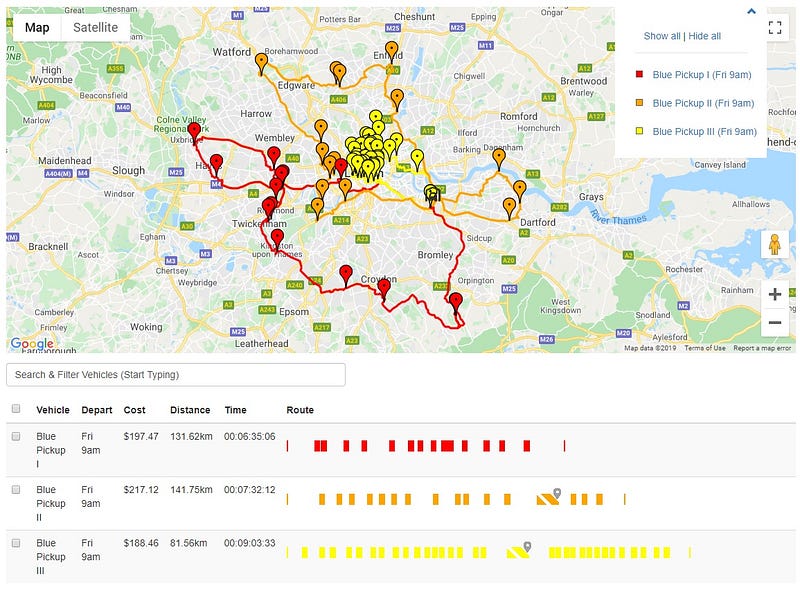
Several efficiencies become apparent here. Blue Pickup II and Blue Pickup III both need to return to the depot to restock due to the requirement to deliver 60 crates with a combined capacity of only 50.

Examining Blue Pickup II’s delivery plan reveals it executes two efficient loops that begin and end close to the depot.

Blue Pickup I manages to deliver 14 crates in a single trip, while Blue Pickup III, with its larger capacity, services more locations than the smaller trucks.

You might wonder if we could minimize the use of Blue Pickup III, which incurs a higher distance cost. However, if you look closely at the distance covered by Blue Pickup III, you will see that it actually travels significantly less than the two less expensive vehicles while handling the bulk of the deliveries. This approach allowed the delivery plan to keep costs down while fully utilizing the larger vehicle's capacity.

As we consider the impact of pickups alongside deliveries, let’s assume we have 50 deliveries and 10 pickups, which means we have 50 crates to deliver and an additional 10 to return to the depot.

Here’s what an optimized route and delivery plan looks like:

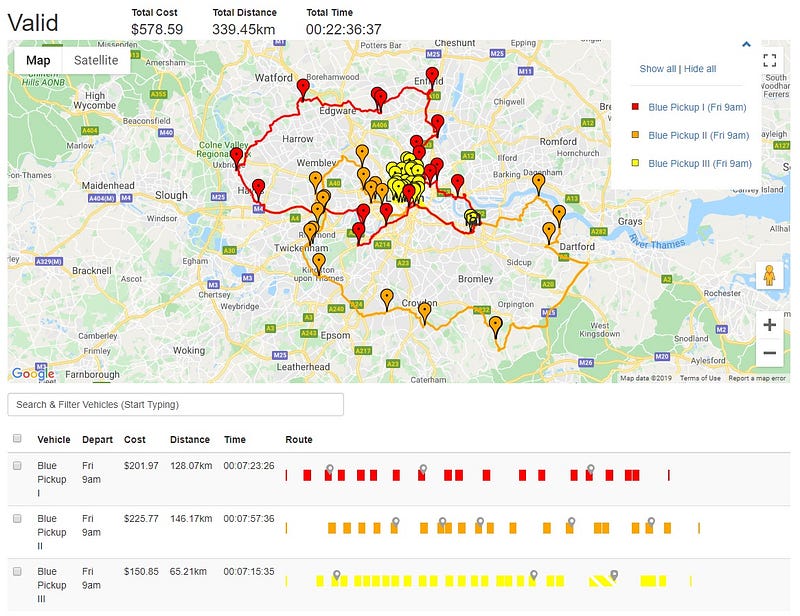
The new schedule is feasible, with all three vehicles completing their trips within the 8-hour time limit. Blue Pickup III makes two trips, while the others manage with just one. Notably, Blue Pickup III still travels about half the distance of the other vehicles, despite returning to the depot.

Blue Pickup II, which holds 15 crates, visits 19 locations in a single trip by making five pickups, while Blue Pickup I departs with 14 crates, leaving a single crate capacity open.

This dual delivery and route optimization enable Blue Pickup III to undertake two efficient routes without compromising on time or distance.

Some readers might wonder about the necessity of multiple trips. If we could make use of the full capacity of Blue Pickup I and II, wouldn’t that eliminate the need for additional trips? However, the locations Blue Pickup III serves are clustered together, requiring a return to the depot for further deliveries.

It's crucial to understand that while it may seem possible to avoid multiple trips, doing so would result in longer travel distances for other vehicles, likely exceeding their scheduled limits and increasing costs significantly.

Ultimately, tackling delivery planning and route optimization involves navigating incredibly complex mathematical challenges to derive the most cost-effective solutions for real-world applications.

Chapter 2: Advanced Route Optimization Techniques

In this insightful video titled "Revolutionize Your Supply Chain: Discover the Ultimate Guide to Solving Transportation Problems," you'll learn innovative strategies for enhancing supply chain efficiency.

The second video, "Operation Research 14: Unbalanced Transportation Problem using Northwest, Least Cost & VAM," delves into advanced techniques for tackling transportation problems.