Chapter 1: The Oxford MAT Experience

Oxford University stands out as a premier institution for mathematics. Each year, a multitude of aspiring students attempt the MAT, aiming to secure a place in its esteemed math programs. Today, we will tackle a calculus challenge from the Oxford MAT 2021 exam.

Here’s a hint: All the emojis used in this context exhibit some form of symmetry.

I suggest pausing here to grab a pen and paper—give this a try! Once you’re ready, continue for the solution.

Section 1.1: Unveiling the Challenge

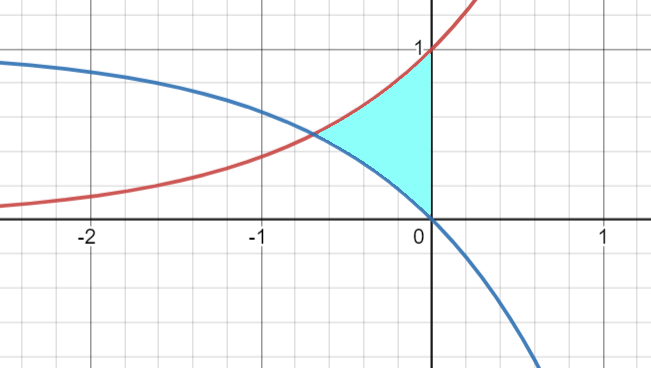
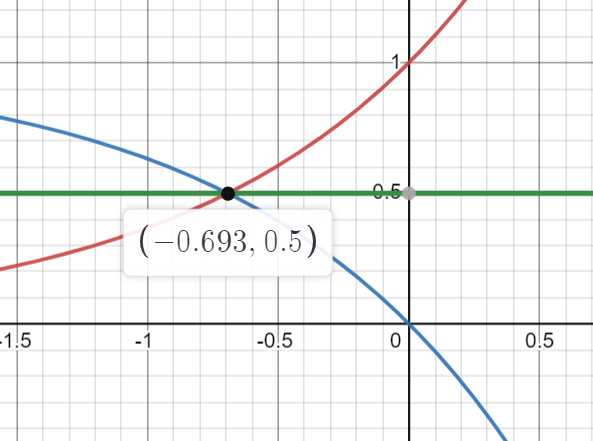
Let’s revisit the graph to find our solution.

The red curve represents e^x, while the blue curve illustrates 1 - e^x. Our task is to determine where these two equations intersect.

The intersection point occurs at:

x = ln(1/2) = ln(2)^-1 = -ln(2)

Let’s substitute this value into y = e^x and analyze the result.

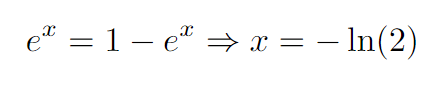
Notice how this value is significant? The horizontal line y = 1/2 perfectly divides the area we intend to calculate.

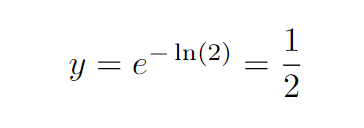
The intersection point we identified is (-ln(2), 1/2).

Section 1.2: Reflecting on Symmetry

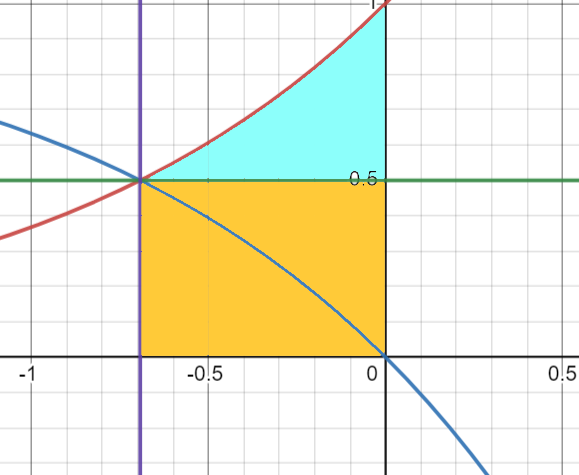
Thanks to the reflectional symmetry of the area, akin to a butterfly’s wings, we can compute half of the region's area and simply double it.

We can determine the blue region by utilizing the orange rectangle formed by the integral under y = e^x: ( A = int ).

Since we’re only calculating half of the area, we multiply by 2 to find the total area of the region.

Mathematically, this gives us:

And there you have it—our solution! Isn’t it fascinating?

What were your thoughts while solving this? I’d love to hear your insights in the comments below!

In the first video, an Oxford mathematician takes on the American AP Calculus BC exam. This challenge showcases the depth and complexity of calculus concepts, illustrating how they are approached in an academic setting.

Chapter 2: A Test of Knowledge

In another intriguing video, an Oxford mathematician presents a rigorous challenge to a physicist using the MAT entrance exam. This highlights the demanding nature of mathematics and its applications.

Thank you for engaging with this content! If you found it helpful, please consider supporting my work. Your encouragement makes a significant difference in my writing journey.

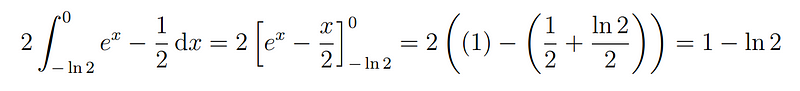
If you appreciate my efforts, feel free to buy me a coffee—it's a wonderful way to support my writing and personal endeavors.

Love, Bella