Analyzing Energy Conservation in Pole Vaulting

When a pole vaulter begins, they run horizontally, gaining kinetic energy. A key question arises: how does this kinetic energy correlate with the gravitational potential energy when reaching the peak of the vault?

According to the work-energy principle, the work performed on a system is equivalent to the change in energy within that system.

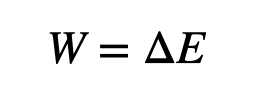
The energy variations depend on how we define our "system." If we include the runner, the pole, and the Earth, we can identify three forms of energy changes: kinetic (K), gravitational potential (U_g), and a type of elastic potential energy stored in the pole. For now, let’s focus on the first two.

When examining gravitational potential energy, it's important to note the variable “y,” which indicates the vertical position. The absolute energy value is less important than the change in energy itself.

To apply the work-energy principle, let’s consider two positions. At Position 1, the vaulter is running horizontally with a speed ( v_1 ) and at a height of 0 meters. At Position 2, the vaulter reaches the peak with a new speed ( v_2 ) and height ( y_2 ). The work-energy equation can then be expressed as follows:

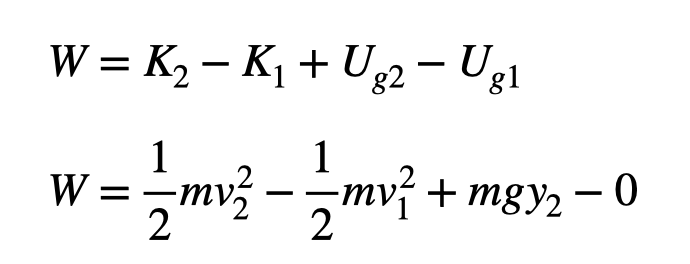
Why is there no elastic potential energy in this equation? At both positions, the pole remains uncompressed, allowing us to sidestep this consideration.

Now, we need to assess the work done on the system. Is the change in kinetic energy sufficient to explain the change in gravitational potential energy? To answer this, we require specific numerical values for velocities and heights.

Pole Vault Video Analysis Methodology

Official Olympic footage is often visually appealing but not necessarily helpful for extracting numerical data. To analyze the pole vault, we need a video that meets certain criteria:

1. A measurable distance scale.
2. A known frame rate (without slow motion).
3. A vantage point that avoids perspective distortions and is perpendicular to the athlete's motion.
4. Minimal panning or zooming.

Fortunately, I discovered a suitable video on Instagram, despite some camera movement.

Using Tracker Video Analysis software, I can establish the height of the bar (6.25 m) as my distance scale. This allows me to adjust the origin point in each frame to account for the camera's movement.

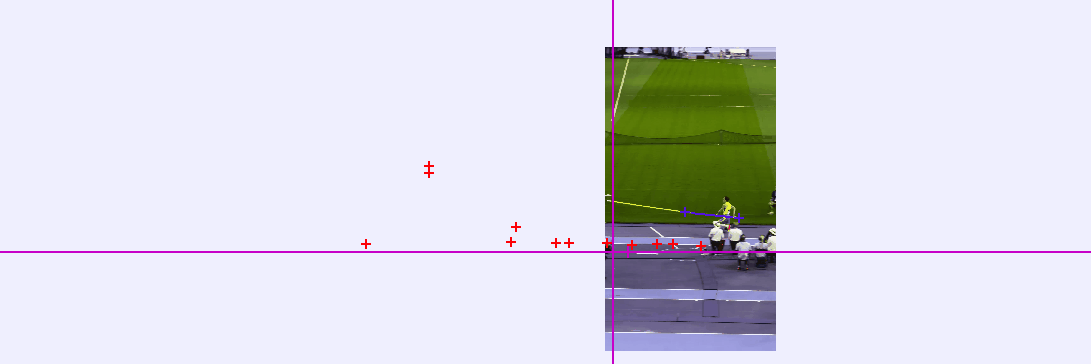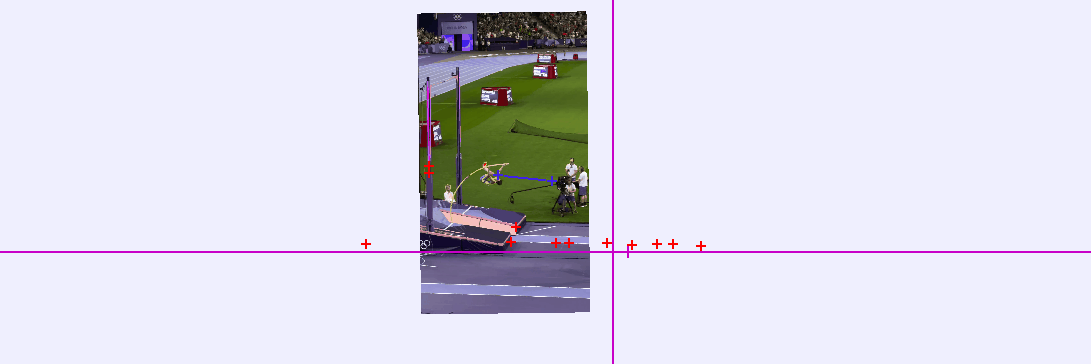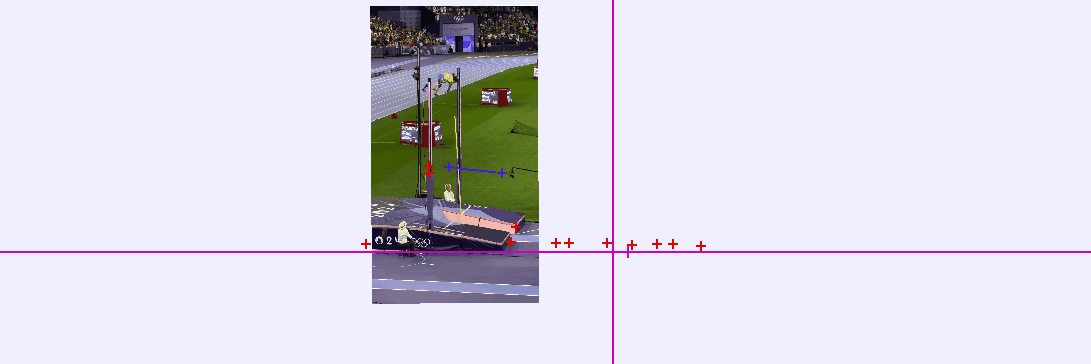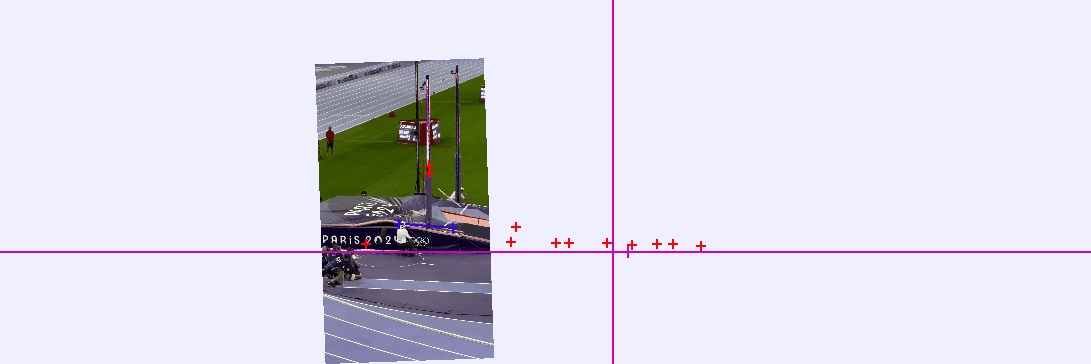
From this analysis, I can derive various critical values, most importantly, the velocities during the vault. Initially, I'll examine Mondo Duplantis as he descends post-vault. Below is a graph illustrating his vertical position over time.

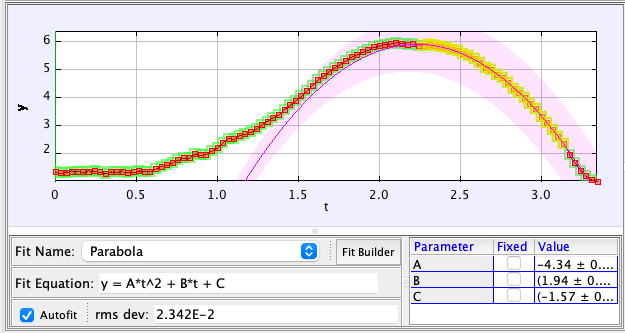
Assuming he falls under the influence of gravity at ( g = 9.8 m/s² ), a quadratic fit should align with the kinematic equation below:

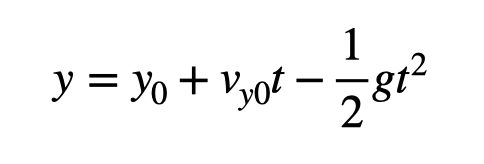
The coefficient before the ( t² ) term should equate to ( 1/2 times g ) or 4.9 m/s², a value that should generally hold true across all Olympic events on Earth. My analysis yielded a coefficient of 4.34 m/s², prompting me to adjust the distance scale until it matched the expected gravitational value.

Next, while assessing the vertical position, I’ll extract an essential measurement. Estimating Mondo’s center of mass, I find he begins at a height of 1.35 meters and reaches 5.96 meters at the peak, resulting in a change of ( Δy = 4.41 ) meters. This indicates that although he cleared a 6.25-meter bar, the change in his center of mass was less significant.

Now, let’s shift our focus to his horizontal position over time.

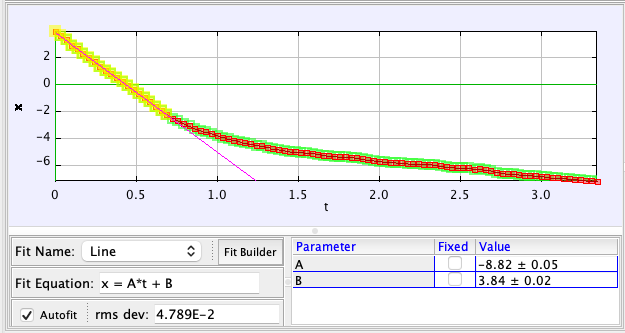
The slope of this graph represents the horizontal velocity. Before the vault, Mondo recorded a speed of 8.82 m/s, which decreased to 1.169 m/s at the apex.

Calculating Work and Energy

To complete our calculations, we need Mondo Duplantis’ weight (mass), which is listed as 174 pounds or 78.9 kilograms on Earth.

Using these values, I computed a work output of 394.9 Joules. This indicates that achieving his record vault required Mondo to contribute an additional 394.9 Joules of energy to the system. Essentially, he utilizes muscular force during the ascent to generate this energy.

Interestingly, this amount of work is relatively minimal, constituting only 11 percent of the change in gravitational potential energy, assuming negligible energy loss through the pole.

Homework Assignment

As this is a physics exploration, here's your assignment:

1. Assume Mondo did not contribute extra energy during his vault. Estimate the height he could clear based solely on his kinetic energy.
2. Analyze the video to approximate the effective spring constant of the pole. This will require estimating how much the pole compresses.
3. Determine what fraction of a candy bar's energy is utilized during the ascent and how much is expended in increasing kinetic energy.

Lastly, note that I didn't factor in the mass of the pole, which affects the overall calculations of the Mondo-pole system. Try recalculating while including the pole's mass for a more comprehensive analysis.

The second video titled "The Physics of a Pole Vault" offers further insights into these principles.