Chapter 1: Introduction to Trigonometry

Trigonometry doesn't have to be a source of confusion; it simply requires a fresh perspective. Visual proofs play a significant role in making concepts clearer, particularly the Inscribed Angle Theorem and the Law of Sines, which are closely interlinked.

Section 1.1: The Inscribed Angle Theorem Explained

In this theorem, the chord AB intersects at the center point C, effectively spanning the circle's diameter. The segments CA, CD, and CB are all radial lines, making them equal in length. Consequently, all angles at point C are right angles. This setup results in two congruent triangles, ACD and BCD, with triangle ABC also being a right triangle, and angle ADB is right as well.

Now, consider what occurs when the diameter segment is rotated around point C.

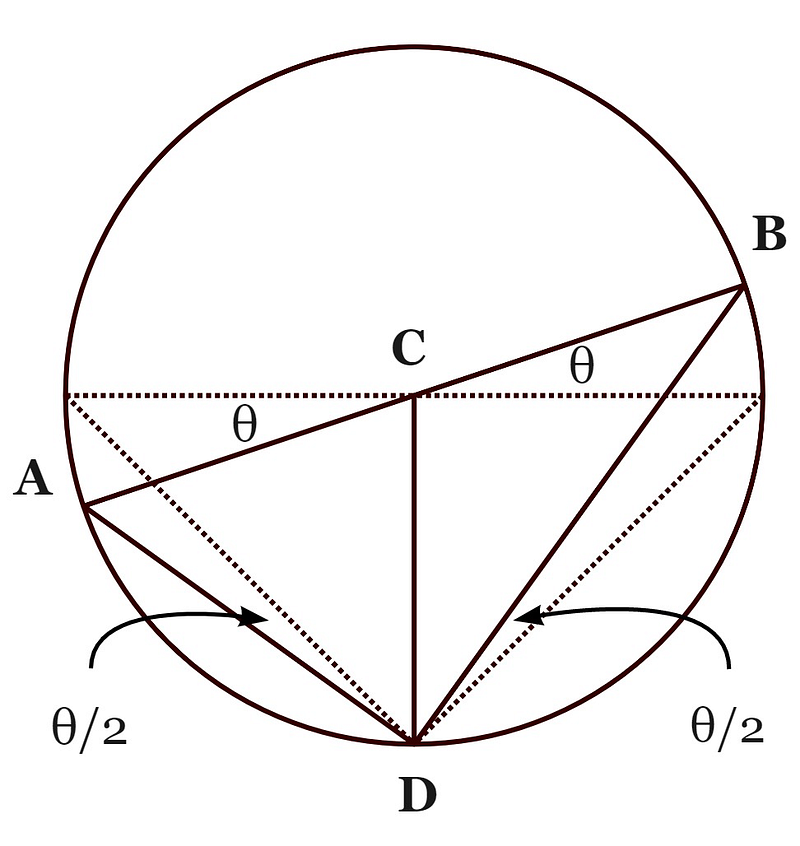
As we pivot the diameter, the two smaller triangles lose their congruency but remain isosceles, with their equal sides being the length of the circle’s radius. The angles at C increase for one triangle while decreasing for the other, yet the sum of these changes remains balanced. Despite these adjustments, angle ADB continues to hold its right angle.

Thus, when a triangle is inscribed within a circle and one side crosses the diameter, that diameter serves as the hypotenuse of a right triangle.

Subsection 1.1.1: Generalization of the Inscribed Angle Theorem

Continuing from our previous point, if we pivot only the radial line CB, the angle at ACB will measure 180 degrees minus some value. The right angle at D will reduce by half of that same value. Hence, angle ADB will perpetually measure half of angle ACB.

This principle also applies if we rotate line AC around point C at a different angle. Therefore, when an angle is formed between two points on the circle and its center, another angle formed between the same two points and a different point outside the first angle will be exactly half of the initial angle.

Chapter 2: The Law of Sines Unveiled

Having laid the groundwork with the Inscribed Angle Theorem, we can seamlessly transition into the Law of Sines.

The first video provides a visual proof of the Law of Sines, illustrating its application in trigonometry.

Consider a triangle inscribed within a unit circle.

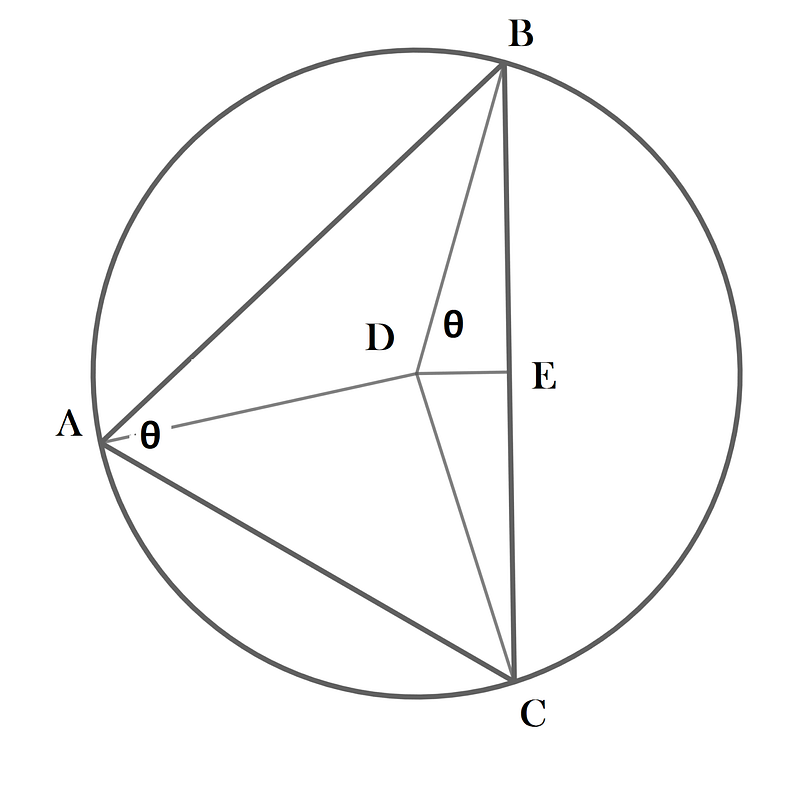
From each vertex of the triangle, we draw lines to the center of the circle, where each side of the triangle acts as a chord. The segment DE bisects the central angle BDC, and according to the Inscribed Angle Theorem, angles BDE and BAC are equivalent.

Since BE represents the sine of angle ?, it follows that the side BC measures twice the sine of its opposite angle, which is also ?. This principle applies universally for every angle in the triangle, establishing that each side's length is double the sine of the angle opposite to it.

Thus, for triangle sides a, b, and c, and their opposing angles A, B, and C:

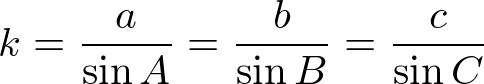
In the context of a unit circle, the constant k equals 2. For other circles, this constant will vary based on the scale of the circle.

The second video covers the Inscribed Angle Theorem, providing proofs and practice problems to reinforce your understanding.

What if point D were positioned on the opposite side of the circle? Can we extend this theorem further to accommodate that scenario?