Chapter 1: Understanding Topological Spaces

In our previous discussion regarding embeddings and immersions, we referenced various aspects of point-set topology. To ensure clarity and accuracy, it's essential to elucidate some of the terminology and definitions associated with subspaces and embeddings.

To begin, we must define what constitutes a topology from the perspective of point-set topology. Following this, we will delve into the notions of continuity, compactness, and the Hausdorff condition.

Topological Spaces and Continuity

A topological space, denoted as (X, ?), consists of a set X along with a collection of subsets ? (referred to as open sets), provided that they adhere to the open set axioms.

When considering a mapping f that connects elements from one topological space to another, we can articulate the concept of continuity through the lens of open maps. Specifically, a mapping f: X → Y is deemed continuous if, for every open subset U in Y, the preimage f^(-1)(U) is an open set in X. The preimage is defined as the collection of all elements in the original space that correspond to points in the target space.

As we explore embeddings and immersions further, it becomes necessary to understand the subspace topology. Given a topological space X and a subset Y of X, the subspace topology comprises open sets that are defined as follows:

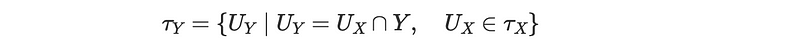
In this context, the inclusion map assigns X to Y, where the domain is equipped with the subspace topology and the range is characterized by the standard topology. Additionally, the inclusion map is continuous because ??1(U_Y) = U_Y ∩ X, within ??_X.

Chapter 2: Subspace Topology and Its Applications

The concepts we've discussed are foundational for grasping more complex ideas in topology. For a deeper understanding of subspace topology, let's explore the following video.

This video titled "Subspace Topology 1 (Topology)" provides a detailed examination of subspace topology and its significance within the broader context of topological spaces.

Continuing our exploration, we will now look at an important problem related to the cross-ratio and subspaces.

The second video, "Cross ratio & 4 subspace problem," delves into the complexities of the cross-ratio in relation to subspaces, further enhancing our understanding of these concepts.