Exploring Heisenberg Transportation: Unveiling New Possibilities
Written on
Chapter 1: Understanding the Heisenberg Group
Imagine a scenario where transporting items transcends simple distance metrics and delves into the very essence of space itself. This is the innovative domain of Heisenberg group transport, a sophisticated mathematical model that redefines traditional Euclidean perspectives. The Heisenberg group, characterized by complex algebraic interrelations, provides a fresh approach to formulating and resolving transportation challenges. This isn't merely a theoretical construct; it has practical implications across diverse fields, including physics and urban development. By optimizing a cost function within this distinct geometry, researchers can identify optimal pathways and solutions that are more efficient and adaptable than ever before.
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: The Concept of Horizontal Divergence
At the heart of Heisenberg group transport lies the notion of horizontal divergence. In contrast to Euclidean spaces, where divergence gauges how vectors disperse, the horizontal divergence within Heisenberg space accounts for the unique structure of the group. The objective is to minimize this divergence while relocating objects between points, necessitating the resolution of intricate equations and the application of probability measures across restricted domains. Through these methods, researchers can uncover the most effective strategies for moving items within the Heisenberg framework, paving the way for enhanced transport efficiency in both theoretical and practical contexts.
Subsection 1.1.1: Visualizing the Heisenberg Group's Geometry

Section 1.2: The Duality of Heisenberg Transport
One of the most intriguing features of Heisenberg group transport is its dual formulation. This involves reconfiguring the original minimization task into a dual maximization challenge. By focusing on the dual framework, researchers can derive richer insights and pinpoint solutions that may otherwise remain elusive. This duality also links the Heisenberg transport issue to other well-established mathematical problems, such as the Monge-Kantorovich problem. Exploring these interrelations enables scientists to devise novel methodologies and tools for addressing a broad spectrum of transport and optimization challenges, thereby broadening the applications of Heisenberg group transport.
Chapter 2: Practical Applications of Heisenberg Transport
The principles of Heisenberg group transport extend well beyond theoretical constructs. They possess substantial real-world relevance, particularly in domains that demand efficient resource movement and distribution. For instance, urban planners can leverage these models to create improved traffic systems, alleviating congestion and enhancing travel efficiency. In the realm of physics, these principles contribute to a deeper understanding of particle dynamics and interactions at fundamental levels. By applying the concepts of Heisenberg transport, researchers can formulate more precise models for various complex systems, leading to advancements in technology and infrastructure.
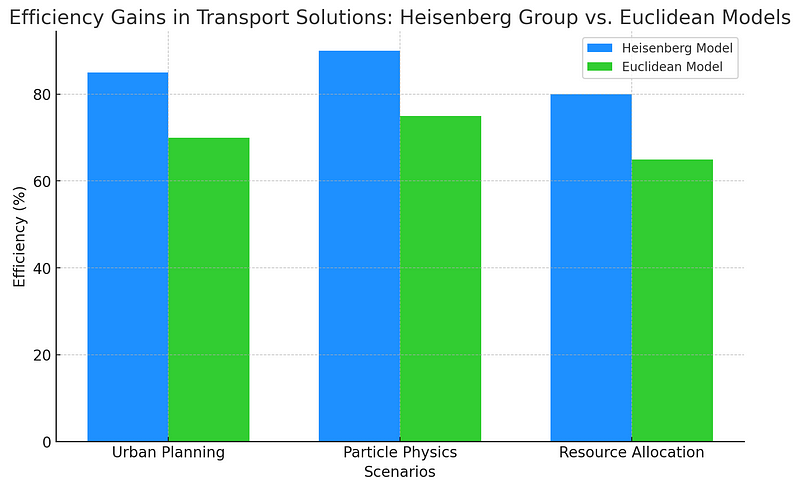
Efficiency Gains Comparison
The graph below compares the efficiency improvements in transportation solutions utilizing the Heisenberg group model against traditional Euclidean frameworks.
Chapter 3: The Future of Transportation Innovations
As our comprehension of the Heisenberg group deepens, the potential for groundbreaking transportation models expands. Future developments may involve increasingly intricate algorithms and computational techniques designed to tackle more complex transport challenges. By persistently investigating and enhancing these models, scientists and engineers can construct more efficient and versatile systems. This not only serves practical needs but also enriches our theoretical grasp of space, movement, and optimization. The Heisenberg group's distinctive characteristics present a promising pathway for future inquiry and innovation, heralding a new age of efficiency and creativity in transportation.
Section 3.1: The Significance of Heisenberg's Unique Geometry
The Heisenberg group defies conventional space concepts. Its geometry, shaped by algebraic relationships, enables the development of more complex and efficient solutions for transport dilemmas, making it an invaluable asset in both theoretical and practical realms.
Section 3.2: Understanding Horizontal Divergence
Horizontal divergence within the Heisenberg group gauges how vectors disperse within this unique framework. Unlike standard divergence, it reflects the specific characteristics of the group, facilitating more precise and efficient transport solutions.
Section 3.3: Advantages of the Dual Formulation
By reformulating transport challenges into their dual counterparts, researchers can unveil new perspectives and solutions. This strategy connects Heisenberg transport with other mathematical inquiries, amplifying its potential applications and offering greater understanding.
Section 3.4: Real-World Implications
The principles of Heisenberg group transport can be employed in urban development, physics, and resource distribution. By optimizing transport within this unique paradigm, we can devise more effective systems for traffic management, particle dynamics, and more.
Section 3.5: Future Potential and Innovations
As research progresses, Heisenberg group transport models will evolve to become even more sophisticated. This promises advancements in computational strategies and algorithms, leading to improved efficiency and adaptability in both practical and theoretical settings.
Chapter 4: The Vision for Heisenberg Transportation
The horizon of transportation shines brightly with the Heisenberg group. By harnessing the capabilities of this exceptional mathematical framework, we have the potential to develop systems that are more efficient, versatile, and insightful. Picture a world where traffic flows effortlessly, resources are allocated optimally, and scientific models are unprecedentedly accurate. Heisenberg transport principles extend beyond mere object relocation; they reshape our understanding of space and efficiency. As we continue to delve into and innovate within this field, the possibilities are boundless. This marks the beginning of a transformative era in transportation, propelled by the insights and applications of the Heisenberg group.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your gateway to the future of technology. Subscribe for insightful videos every Saturday!
Watch us on YouTube