Chapter 1: Introduction to the Three Square Geometry Problem

The intriguing Three Square Geometry Problem was featured in a 2014 Numberphile video, which remains one of my favorites even after eight years! You can find the link at the end of this article.

The challenge posed is to determine (and prove) the sum of three angles, denoted as ?, ?, and ?, formed by three adjacent squares, illustrated in the accompanying diagram.

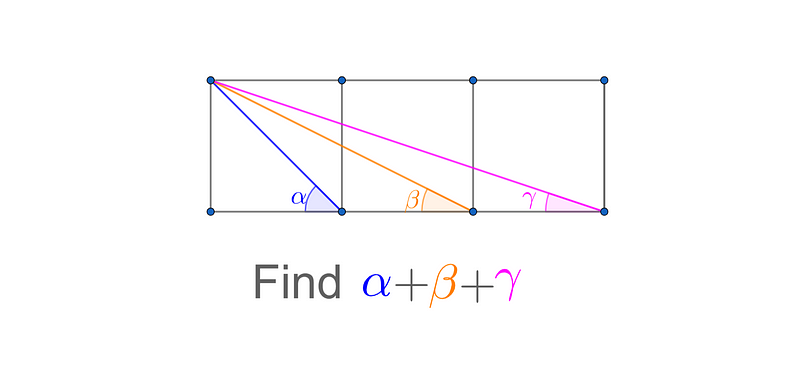
It’s evident that angle ? equals 45° since it corresponds to the diagonal of a square. A quick estimation with a protractor suggests that ? + ? + ? totals 90°. But how do we substantiate this claim? In the Numberphile video, Professor Zvezdelina Stankova recounts how she encountered this problem during her elementary education and presents a clever geometric construction to reach a solution.

However, in this article, I will utilize a proof involving complex numbers. This approach is deemed "elementary" because it relies solely on fundamental principles of complex number arithmetic: the imaginary unit i is defined such that i² = -1, complex numbers can be visualized as points on the x,y plane, and multiplying complex numbers results in an anti-clockwise rotation, as depicted in the following diagram.

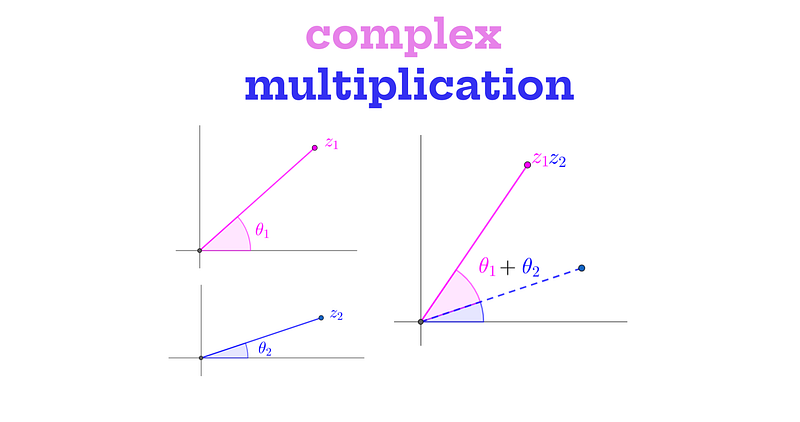
The angle of the product corresponds to the sum of the individual angles (from the x-axis). The relationship between complex multiplication and angle addition might not be immediately apparent (for a deeper insight, see this discussion). Yet, this property is one of the reasons complex numbers are so advantageous!

Section 1.1: The Elementary Complex Solution

For our problem involving three squares, we can utilize the fact that the angles ?, ?, and ? can be represented as the angles from the x-axis of the complex numbers (1 + i), (2 + i), and (3 + i) respectively.

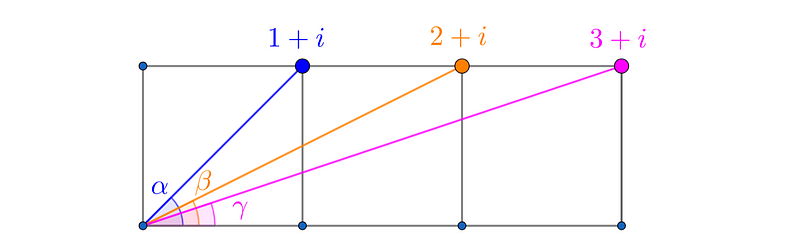
As previously established, angle ? is 45°, due to it being the diagonal of a square. Therefore, the cumulative total of the three angles can be expressed as (45° + ? + ?). To calculate (? + ?), we multiply the complex numbers (2 + i) and (3 + i):

(2 + i)(3 + i)

= 6 + 2i + 3i + i²

= 6 + 2i + 3i - 1

= 5 + 5i

Can you discern the outcome? The angle between the complex number (5 + 5i) and the x-axis also represents the diagonal of a square (with a side length of 5), leading to the conclusion that the sum (? + ?) is also 45°. Thus, the overall total of the three angles becomes 45° + 45° = 90°.

Chapter 2: Conclusion

For a deeper exploration of the Three Square Geometry Problem, check out the Numberphile video linked below.

The first video titled "A Hard Problem in Elementary Geometry" provides additional insights into this fascinating topic.

The second video, "A Hard Problem in Elementary Geometry: Second Attempt," offers a different perspective and further discussion on the problem.